Математика в нардах: как удваивать и принимать удвоение

Нарды – это, главным образом, игра математических ожиданий. Ваши шансы на успех зависят от того, как хорошо вы умеете оценивать вероятность того или иного события в данной ситуации. Можно сказать так – в игре нарды ваши решения хороши настолько, насколько хороши ваши суждения о ситуации, насколько хороши ваши расчеты вероятности выигрыша одной из сторон.

Обосновать решения об удвоении и принятии удвоенией довольно сложно, так как следует принять во внимание эквити матча (от англ. equity – доля в капитале) и применить формулу:

РИСК/ (РИСК + ВЫИГРЫШ)

Немногие смогут держать в голове такие цифры и одновременно производить подсчеты.

Данная статья поможет вам разобраться с этими вопросами.

Эквити матча в нардах

К матчу, который длится до 11 очков применима формула Рика Яновского:

Эквити матча = 50 + ((D/85)/(T+6))%

где D – разница в очках между текущим лидером матча и догоняющим, T – число очков, которое еще надо набрать догоняющему, чтобы выиграть матч

Корректировка была применена, чтобы принять во внимание Правило Кроуфорда при счете матча близком к финальному.

 

Таблица эквити:

 

	1	2	3	4	5	6	7	8	9	10	11
1	50	70	75	83	85	91	92	94	96	97	98
2	30	50	59	67	74	80	84	87	90	92	95
3	25	41	50	59	68	71	76	80	84	87	90
4	17	33	41	50	58	64	70	74	78	82	85
5	15	20	35	42	50	57	63	68	73	77	80
6	9	27	29	36	43	50	57	62	67	71	75
7	8	16	24	30	37	43	50	56	61	66	70
8	6	14	20	26	32	38	44	50	56	61	65
9	4	10	16	22	27	33	39	44	50	55	60
10	3	8	13	18	23	29	34	39	45	50	55
11	2	5	10	15	20	25	30	35	40	45	50

 

Посмотрим на примере

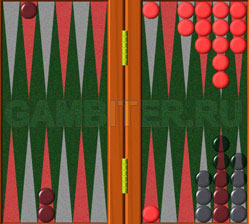
Матч до 9 очков. Черные 7 — Белые 5.

Белые ходят. Действия куба?

 

Белые удвоили, черные сдались.

 

Это было неверное решение, опираясь на математику нужно было принять удвоение. Счет 7-5 до 9 очков: 2 осталось черным, 4 белым. Если белые сдаются, то получится 2 осталось черным, 3 белым. По таблице эквити видно, что шансы черных на победу равны 59%.

 

Математические ожидания со стороны черных:

• Если черные принимают и выигрывают, счет становится 9-6, 100% шансы выигрыша.
• Если черные принимают и проигрывают, счет становится 7-7, 50% шансы выигрыша.
• ВЫИГРЫШ от принятия удвоения составляет 100%-59% = 41%
• РИСК от принятия и поражения составляет 59%-50% = 9%

 

Точка принятия удвоения = РИСК/ (РИСК+ВЫИГРЫШ)=9/(9+41)% = 18%

Могут ли черные победить в конкретной игре из этой позиции в 18% всех случаев? Если да, то удвоение стоит принимать.

Snowie подтверждает это, рассчитав шансы черных на победу в 33%.

 

Давайте теперь посмотрим на удвоение с позиции белых.

Если бы он не удвоил и победил, то счет стал бы 7-6 (2 осталось, 3 осталось) с шансами победить в матче 41%.

Математические ожидания со стороны белых:

• Если белые не удваивают и проигрывают, счет становится 8-5 (1, 4). 17% шансы выигрыша
• Если белые удваивают и выигрывают, счет становится 7-7. 50% шансы выигрыша
• Если белые удваивают и проигрывают, счет становится 9-5, 0% шансов.
• ВЫИГРЫШ от удвоения составляет 50%-41% = 9%, РИСК = 17-0=17%

 

По формуле получается 17 / (17+9) = 17 / 26 = 65%. У белых нет 65% вероятности выиграть эту игру, поэтому им не стоит удваивать.

 

Конечно во время игры в нарды, большинство из нас не смогут провести быстрые вычисления в голове и принять правильное решение, но после игры стоит анализировать такие критические ситуации, чтобы в будущем автоматически принимать правильные решения.

 

Рой Холландс